Leetcode Problem 1335 - Minimum Difficulty of a Job Schedule

 1335. Minimum Difficulty of a Job Schedule

Hard

, Dynamic Programming

You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the ith job, you have to finish all the jobs j where 0 <= j < i).

You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done on that day.

You are given an integer array jobDifficulty and an integer d. The difficulty of the ith job is jobDifficulty[i].

Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.

 

Example 1:

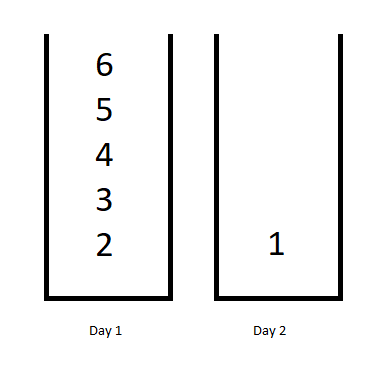
Input: jobDifficulty = [6,5,4,3,2,1], d = 2
Output: 7
Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7 

Example 2:

Input: jobDifficulty = [9,9,9], d = 4
Output: -1
Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.

Example 3:

Input: jobDifficulty = [1,1,1], d = 3
Output: 3
Explanation: The schedule is one job per day. total difficulty will be 3.

 

Constraints:

• 1 <= jobDifficulty.length <= 300
• 0 <= jobDifficulty[i] <= 1000
• 1 <= d <= 10

To solve this problem efficiently using dynamic programming (DP), we need to approach it by dividing the list of jobs into d non-empty subarrays. The problem is about finding the minimum difficulty schedule, where the difficulty of each subarray is the maximum difficulty of the jobs scheduled on that day.

Problem Breakdown:

• We are tasked with dividing the jobs into d groups (or days). Each group must contain at least one job.
• The difficulty of a day is the maximum difficulty of any job assigned to that day, and the total difficulty of the schedule is the sum of the maximum difficulties across all days.

Approach:

Dynamic Programming Approach:

We'll use a 2D DP array dp[i][j] where:

• i represents the number of jobs considered.
• j represents the number of days used to schedule the first i jobs.
• dp[i][j] will store the minimum difficulty for scheduling the first i jobs into j days.

Steps:

1. Base Case:

   • dp[0][0] = 0: No jobs, no days, zero difficulty.
   • dp[i][0] = infinity for i > 0: Impossible to schedule jobs with zero days.
   • dp[i][j] = infinity initially for all other values, indicating impossible cases.

2. DP Transition:

   • For each possible number of days j, and for each possible last job i in the partition, we calculate the difficulty of the current day. This is done by considering all jobs from some earlier job k to i as part of the last day and computing the maximum difficulty for that day.
   • For each partition from k to i, update dp[i][j] as: $$dp[i][j] = \min(dp[i][j], dp[k][j-1] + \text{max difficulty from job } k \text{ to job } i)$$
   • This way, we try to partition the jobs into j groups, calculating the difficulty of each partition.

3. Final Answer:

   • After filling the DP table, the result will be in dp[n][d] where n is the total number of jobs and d is the number of days.

4. Edge Case:

   • If the number of jobs is less than the number of days (n < d), return -1 because it's impossible to schedule jobs.

Code Implementation:

public class Solution {
    public int MinDifficulty(int[] jobDifficulty, int d) {
        int n = jobDifficulty.Length;
        
        // Edge case: If there are fewer jobs than days, return -1
        if (n < d) return -1;
        
        // DP array where dp[i][j] represents the minimum difficulty of scheduling first i jobs into j days
        int[,] dp = new int[n + 1, d + 1];
        
        // Initialize the dp array with a large number (int.MaxValue)
        for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= d; j++) {
                dp[i, j] = int.MaxValue;
            }
        }
        
        // Base case: 0 jobs and 0 days results in 0 difficulty
        dp[0, 0] = 0;
        
        // Iterate over number of days
        for (int j = 1; j <= d; j++) {
            // Iterate over number of jobs to be scheduled
            for (int i = j; i <= n; i++) { // Need at least 'j' jobs to schedule 'j' days
                int maxJobDifficulty = 0;
                // Try partitioning the jobs in different ways
                for (int k = i - 1; k >= j - 1; k--) {
                    maxJobDifficulty = Math.Max(maxJobDifficulty, jobDifficulty[k]);
                    dp[i, j] = Math.Min(dp[i, j], dp[k, j - 1] + maxJobDifficulty);
                }
            }
        }
        
        // The answer is the minimum difficulty of scheduling all jobs in 'd' days
        return dp[n, d];
    }
}

Explanation:

1. DP Table Initialization:

   • We initialize a DP table dp[n+1][d+1] with a very large value (int.MaxValue) to indicate that a schedule is not possible for that configuration. We also set the base case dp[0][0] = 0, as there is no difficulty when there are no jobs and no days.

2. DP Transitions:

   • We iterate over each possible day count (j), and for each day, we check how to split the first i jobs into j groups. We consider each possible partition from k to i, where k is the job index before the current partition.
   • For each partition, we compute the maximum job difficulty for the jobs assigned to that day and add it to the previous day's difficulty (dp[k][j-1]).

3. Final Answer:

   • Once all the DP table entries are filled, dp[n][d] holds the minimum possible difficulty for scheduling all n jobs into d days.

Time Complexity:

• Time Complexity: O(n * n * d). We have three nested loops:
  • The outer loop runs d times (for the days).
  • The second loop runs n times (for the jobs).
  • The innermost loop runs up to n times (to check all possible previous jobs in the current partition).
• Space Complexity: O(n * d) for the DP table.

Example Walkthrough:

Example 1:

Input:

jobDifficulty = [6, 5, 4, 3, 2, 1], d = 2

Output:

7

• Day 1: Jobs [6, 5, 4, 3, 2] (max difficulty = 6).
• Day 2: Jobs [1] (max difficulty = 1).
• Total difficulty = 6 + 1 = 7.

Example 2:

Input:

jobDifficulty = [9, 9, 9], d = 4

Output:

-1

• More days than jobs, so it's impossible to schedule.

Example 3:

Input:

jobDifficulty = [1, 1, 1], d = 3

Output:

3

• Each day gets one job, and the difficulty of each day is 1.
• Total difficulty = 1 + 1 + 1 = 3.

This dynamic programming approach ensures that we explore all valid job partitions while optimizing for the minimum difficulty. Let me know if you have more questions!